ГДЗ до підручника «Геометрія» О.С. Істера. 7 клас

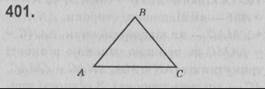
Нехай в △АВС AB = BC. За властивістю кутів рівнобедреного трикутника ∠BAC = ∠BCA. AB = AC, тоді ∠ABC = ∠ACB. Отже, маємо ∠BAC = ∠BCA = ∠АВС. Оскільки сума кутів трикутника дорівнює 180°, то ∠BAC = ∠ВСА = ∠АВС = 180° : 3 = 60°.

Відповідь: 60°.

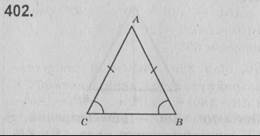
Нехай △АВС — рівнобедрений, АС = АВ, ∠АСВ = ∠АВС = 70°.

Оскільки сума кутів трикутника дорівнює 180°, маємо: ∠САВ = 180° - (∠АСВ + ∠АВС) = 180° - (70° + 70°) = 180° - 140° = 40°.

Відповідь: 40°.

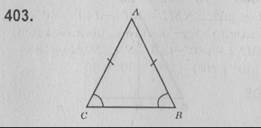
Нехай △АВС — рівнобедрений, АС = АВ, ∠АСВ = ∠АВС = 45°. За теоремою про суму кутів трикутника маємо: ∠САВ = 180° - (∠АСВ + ∠АВС) = 180° - (45° + 45°) = 180° - 90° = 90°.

Відповідь: 90°.

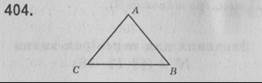
Нехай △АВС — рівнобедрений, АС = АВ, ∠САВ = 80°. ∠АСВ = ∠АВС — як кути при основі рівнобедреного трикутника. ∠САВ + ∠АСВ + ∠АВС = 180°, ∠АСВ + ∠АВС = 180° - 80° = 100°. Отже, ∠АСВ = ∠АВС = 100° : 2 = 50°.

Відповідь: 50°.

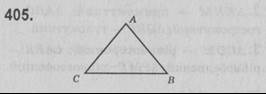
Нехай △АВС — рівнобедрений, АС = АВ, ∠САВ = 50°. ∠АСВ = ∠АВС — як кути при основі рівнобедреного трикутника. ∠САВ + ∠АСВ + ∠АВС = 180°, ∠АСВ + ∠АВС = 180° - 50° = 130°. Отже, ∠АСВ = ∠АВС = 130° : 2 = 65°.

Відповідь: 65°.

406. Мал. 299. ∠АВС = 70° (як вертикальний кут з кутом, який дорівнює 70°). ∠САВ = 180° - (∠АСВ + ∠АВС) = 180° - (80° + 70°) = 180° - 150° = 30°.

Мал. 300. ∠ВСА = 180° - 135° = 45° (як суміжний кут з кутом, який дорівнює 135°). ∠АВС = 180° - (∠ВАС + ∠ВСА) = 180° - (75° + 45°) = 180° - 120° = 60°.

407. Мал. 301. ∠LMN = 50° (як вертикальний кут з кутом, рівним 50°). ∠LNM = 180° - (∠MLN + ∠LMN) = 180° - (70° + 50°) = 60°.

Мал. 302. ∠NML = 180° - 140° = 40° (як суміжний кут з кутом, рівним 140°). ∠MNL = 180° - (∠MLN + ∠NML) = 180° - (50° + 40°) = 180° - 90° = 90°.

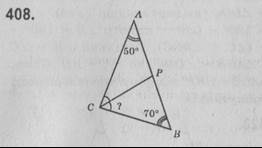
У △АВС ∠А = 50°, ∠В = 70°. ∠С = 180° - (∠А + ∠В) = 180° - (50° + 70°) = 180° - 120° = 60°. Оскільки СР — бісектриса кута С, то ∠АСР = ∠РСВ = 60° : 2 = 30°.

Відповідь: 30°.

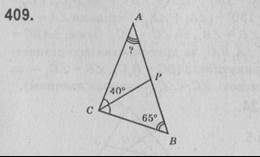
У △АВС ∠В = 65°, ∠АСР = 40°. Оскільки СР — бісектриса кута С, то ∠АСВ = 2∠АСР = 2 • 40° = 80°. Отже, ∠А = 180° - (∠АВС + ∠АСР) = 180° - (65° + 80°) = 180° - 145° = 35°.

Відповідь: 35°.

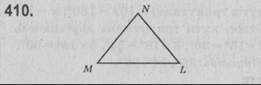
У трикутнику MNL ∠М + ∠N = 120°, ∠М + ∠L = 140°. ∠М + ∠N + ∠L = 180° — як сума кутів трикутника. ∠L = 180° - (∠M + ∠N) = 180° - 120° = 60°, ∠M = 140° - ∠L = 140° - 60° = 80°, ∠N = 120° - ∠М = 120° - 80° = 40°.

Відповідь: 60°, 80°, 40°.